Code

Demo Code and a short tutorial for the EM-WaveHoltz method

Demo code for a simple 1D problem

The Demo code is written to showcase how to couple EM-WaveHoltz with a time-domain solver: julia version matlab version

The matlab demo code is written by me and Dr. Pengliang Yang. Great thanks to Pengliang for his suggestions.

If you read our sample code, you may notice that we only fiter the electric field. The reason is that we are considering a simple problem with $\textrm{Im}(H)=0$. For more complicated problems, we need to filter both electric and magnetic fields.

1 Basic Ideas

2 How to adapt your time-domain code to solve a frequency-domain problem?

3 Properties of WaveHoltz and more remarks

4 Reference

Basic ideas

Given the frequency-domain problem, such as the following simple non-dimensionalized case: $\begin{align} &i\omega E = \nabla\times H-J,\\ &i\omega H = -\nabla\times E. \end{align}$ We define a time-domain problem $\begin{align} &\partial_t \tilde{E} = \nabla\times \tilde{H}- \sin(\omega t)\textrm{Re}(J)-\cos(\omega t)\textrm{Im}(J),\\ &\partial_t \tilde{H} = -\nabla\times \tilde{E}， \end{align}$ and a filtering operator acting on the initial condition of the time-domain problem $\begin{align} \Pi \left(\begin{matrix} \tilde{E}_0\\ \tilde{H}_0 \end{matrix}\right) =\frac{2}{T}\int^{T}_{0}\left(\cos(\omega t)-\frac{1}{4}\right) \left(\begin{matrix} \tilde{E}(t)\\ \tilde{H}(t) \end{matrix}\right) dt,\quad T=\frac{2\Pi}{\omega}. \end{align}$ $\Pi\nu$ essentially filters the time-domain solution determined by the initial condition $\nu$ over one period.
With some simple algebra, one can show that $\begin{align} \Pi \left(\begin{matrix} \textrm{Im}(E)\\ \textrm{Im}(H) \end{matrix}\right)= \left(\begin{matrix} \textrm{Im}(E)\\ \textrm{Im}(H) \end{matrix}\right). \end{align}$

Hence, solving the frequency-domain problem is equivalent to solve the fixed point problem $ \Pi\nu = \nu$ in the time-domain.

To solve this time-domain fixed point problem, we have two choices.

Apply fixed point iteration/Anderson acceleration.
Rewrite the $\Pi\nu = \nu$ as an equivalent linear system $(I-S)\nu = \Pi 0,\;\text{with}\;S\nu = \Pi \nu -\Pi 0,$ and solve it with an iterative solver.

Remark: Matrix vector multiplication $(I-S)\nu$ can be computed in a matrix-free manner based on a time-domain solver. We also want to point that $\Pi 0$ filters the solution corresponding to $0$ initial condition over one period and with non-zero source $\Pi 0\neq 0$.

How to adapt your time-domain code to solve a frequency-domain problem?

Eessential new components include:

An integration in time to compute the result of the filtering operator,
A function to wrap matrix-vector multiplication in matrix free format.

The filtering operator $\Pi$ can be implemented by adding a few lines (e.g. the red lines below) to your time-domain solver.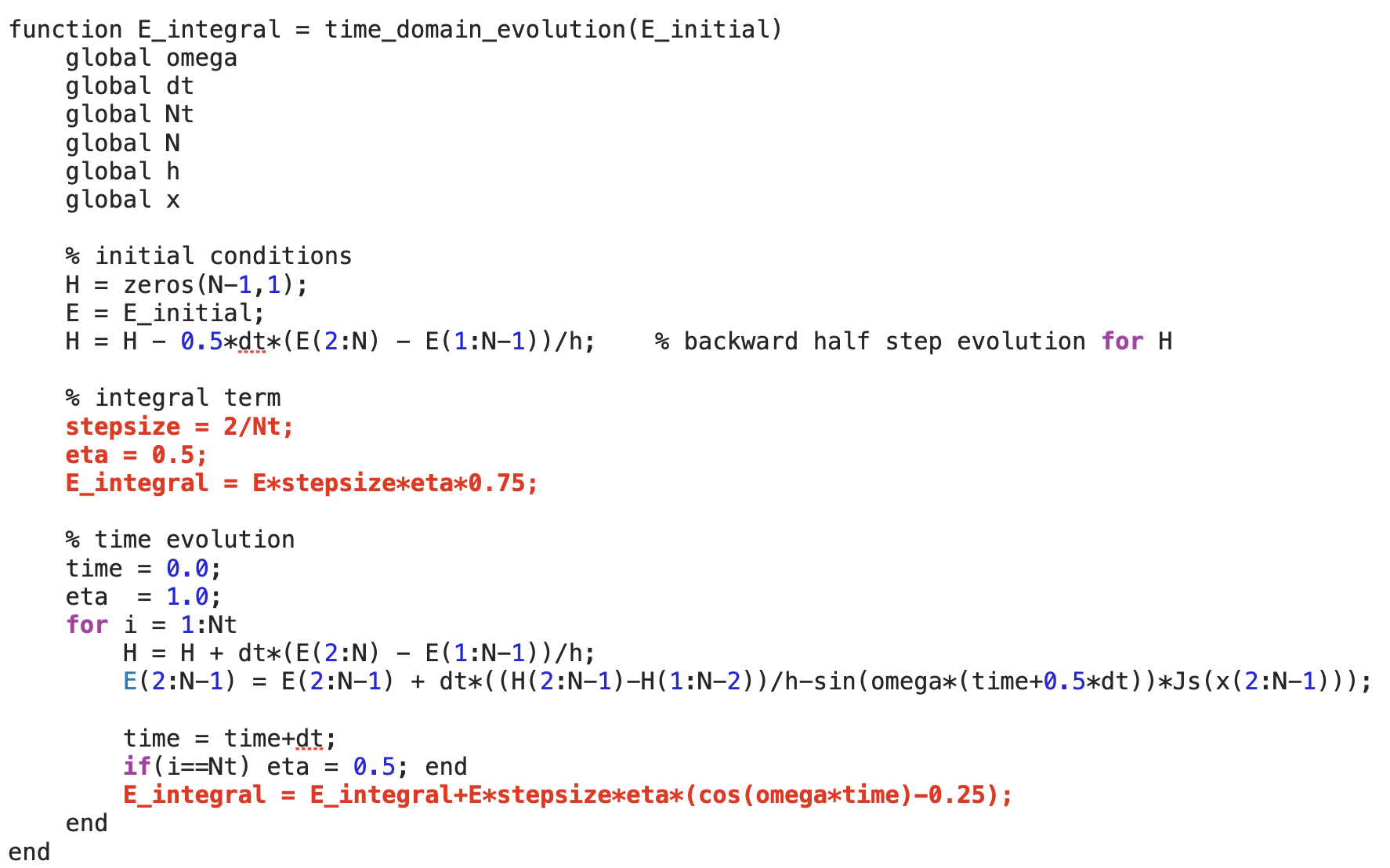

Then, we can compute the right hand side vector $\Pi 0$ and the matrix-vector multiplication $(I-S)\nu$ in a matrix free manner.

PI_0 = time_domain_evolution(zeros(N,1));% compute PI 0

% Operator (I-S)v = (I-Π)v + Π0
%===============================
function res = ImS(v)
    % use time domain simulation to compute Πv
    global PI_0;
    PI_v = time_domain_evolution(v);
    res = v-PI_v+PI_0;
end

At the end of the day, we can solve $(I-S)\nu = \Pi 0$ with a Krlov subspace iterative solver.

Remark: An alternative implementation of $S\nu=\Pi\nu-\Pi 0$ is to set the initial condition as $\nu$ and the source term as $0$ in the time-domain. This alternative implementation is based on the following facts. $\Pi \nu$ filters the time-domain solution with initial condition $\nu$ and the source $-\widetilde{J}(t)=-\sin(\omega t)\textrm{Re}(J)-\cos(\omega t)\textrm{Im}(J)$ and $\Pi 0$ filters the time-domain solution with zero initial condition and the same source. Because the time-domain problem is linear, $\Pi \nu -\Pi 0$ equals to filtering the time-domain solution with the initial condition $\nu=\nu-0$ and the source $0=-\widetilde{J}-(-\widetilde{J})$.

Properties of WaveHoltz and more remarks

To some extent, WaveHoltz can be seen as preconditioning the frequency-domain problem with time-domain simulations and filtering.
In comparsion with limiting amplitude principle, the filtering process makes the convergence faster. Additionally, the WaveHoltz method can be applied to problems in the closed domain (e.g. PEC boundary conditions for all boundaries).
Number of iterations for solving $(I-S)\nu=\Pi 0$ with a Krylov solver:
- Independent of points per wavelength.
- With a fixed number of points per wave length, it scales as $O(\omega)$ for problems without trapped wave structures (e.g. Mie scattering with non-refelcting boundary conditions) and $O(\omega^d)$ ($d$ is the dimension of the problem) for the worst case with fully trapped wave structures (e.g. a problem with PEC boundary conditions for all boundaries).
For the energy conserving problem with PEC boundary conditions, real current $J$, real permitivity and real permeability, the resulting linear system is symmetric positive definite (SPD). Note that for other cases, the resulting linear system may not be SPD. For example, in the case with non-reflecting boundary conditions, the linear system has complex eigenvalues.
It is possible to compute solution corresponding to multiple frequencies with one linear solve and post-processing. See our paper for details.

Reference

Daneil, Fortino and Olof’s first WaveHoltz paper for the Helmholtz equation: D. Appelö, F. Garcia, O. Runborg, WaveHoltz: Iterative Solution of the Helmholtz Equation via the Wave Equation, SIAM Journal on Scientific Computing, Vol. 42, 4, A1950-A1983
Our paper for the frequency-domain Maxwell’s paper: Z. Peng, D. Appelö, EM-WaveHoltz: A flexible frequency-domain method built from time-domain solvers, IEEE Transactions on Antennas and Propagation, 2022, Vol. 70, 7

Zhichao Peng